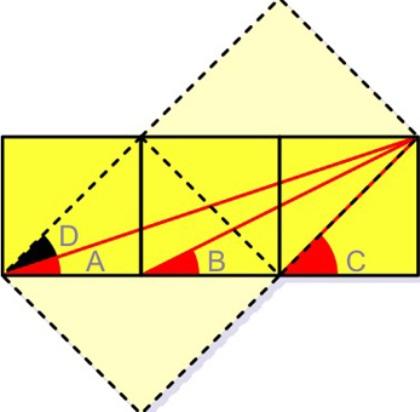
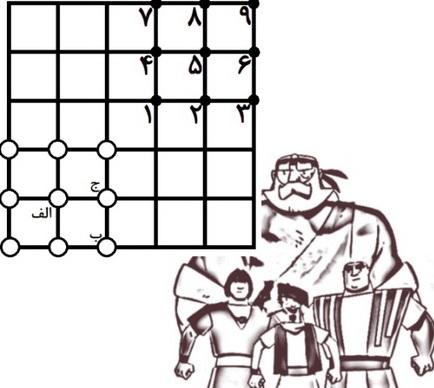
در تصویر زیر کدام رابطه میان زوایههای A و B و C برقرار است؟

۱: 2B - A = C
۲: 2A - B = C
۳: A - B = C
۴: A + B = C
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
♦♦♦♦♦
پاسخ معمای زاویههای مجاور :
ابتدا یک مستطیل جدید ایجاد کرده و آن را به صورت زیر بر روی مستطیل اصلی قرار میدهیم. میدانیم که جمع زاویههای A و D برابر با زوایه C است. چرا که مستطیل دوم مربع کوچک سمت راست را به صورت قطری به دو زوایه مساوی تقسیم کرده است و در واقع طولهای مستطیل دوم، دو خط موازی محسوب میشوند.
زاویه B با زاویه D برابر است. به بیان دیگر زاویه سمت راست مستطیل دوم، که در مقابل زاویه D قرار گرفته و حاصل از قطع کردن مستطیل اصلی است، همان زاویه B است. پس میتوان زاویهی B را جایگزین زاویه D کرد.
بر همین اساس، به این نتیجه میرسیم که پاسخ برابر با گزینهی ۴ یعنی برابر A + B = C است.