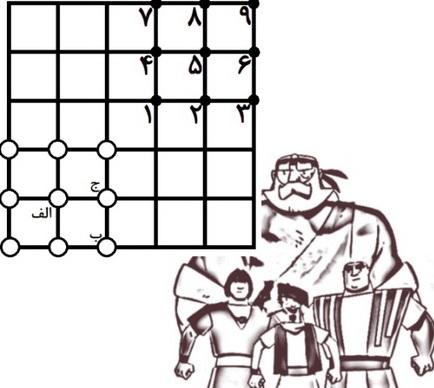
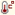پهلوان پوریای ولی از یاور خواسته که ۹ میل زورخانه را از نقاطی که با دایره توخالی نمایش داده شده به نقاطی که با دایره توپر نمایش داده شده ببرد، به نحوی که مجموع فواصل ۹ جفت نقطه ابتدایی و انتهایی، بیشترین مقدار ممکن شود. (دقت کنید که در هر نقطه یک میل قرار می گیرد.)

در این صورت میل های الف و ب و ج به ترتیب باید به کدام نقاط منتقل شوند؟

1) 2،3،5

2) 8،7،5

3) 8،7،9 

4) 4،7،5

5) نمیتوان تعیین کرد

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

پاسخ معمای المپیادی:

پاسخ: ۵

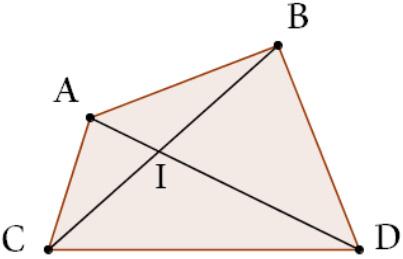
لم: در هر چهار ضلعی محدب مجموع طول قطرها از مجموع طول دو ضلع روبرو بیشتر است.

با نوشتن نامساوی مثلث برای مثلث های ABI و CDI مشاهده می کنیم که: AD + BC > AB + CD

ادعا می کنیم اگر مجموع فواصل ۹ زوج نقطه بیشترین مقدار شود، باید هر دو مسیری بین نقاط ابتدایی و انتهایی همدیگر را قطع کنند. زیرا اگر میل نقطه A به B و میل نقطه C به D برود و AB و CD برخورد نداشته باشند، طبق لم بالا با بردن میل نقطه A به D و میل نقطه C به B مسیر بیشتری طی می شود. حال به میل نقطه ب در صورت سوال نگاه کنید. این میل تنها به نقطه ای ۷ می تواند منتقل شود تا با تمام مسیرها برخورد داشته باشد. (اگر به این نقطه نرود با مسیری که به نقطه ۷ می رسد برخورد ندارد.) پس نقطه ب به نقطه ۷ می رود.

به همین شکل شمال غربی ترین میل نیز باید به نقطه ۳ برود. به همین طریق می توان بررسی کرد که میل های نقاط ج، بالا، پایین و سمت راست الف نیز باید به ترتیب به نقاط ۶ ،۲ ،۴ و ۸ بروند تا با تمام خطوط دیگر برخورد کند اما میل های روی قطر مربع باقی می مانند. این میل ها به هر ترتیبی به نقط ۵ ،۱ و ۹ منتقل شوند مجموع جابه جایی ثابت می ماند. بنابراین برای جای گذاری میل نقطه الف سه حالت وجود دارد و به طور یکتا مشخص نمی شود.