شش عنکبوت با شماره های ۱ تا ۶ روی تار عنکبوتی به شکل بالا زندگی می کنند. هر عنکبوت دقیقا با سه عنکبوت دیگر همسایه است. برای مثال عنکبوت ۱ با عنکبوت های ۲و ۴و ۶ همسایه است.

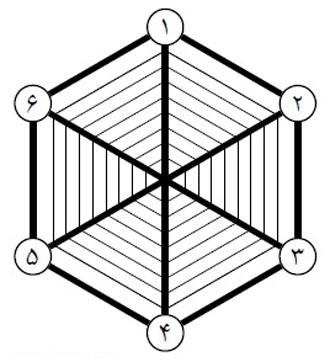
در ابتدای روز هر عنکبوت روی در خانه اش، شماره‌اش را می نویسد. سپس در هر ساعت هر کدام از عنکبوت ها عدد نوشته شده روی در خانه اش را پاک می کند و به جای آن مجموع اعداد همسایه هایش را می نویسد.

مثلا بعد از گذشت یک ساعت روی در خانه ی عنکبوت شماره ی ۲ عدد ۹ نوشته می شود. پس از گذشت ۴ ساعت، مجموع اعداد نوشته شده روی همه ی خانه ها چند است؟

الف) ۱۹۱۹         ب) ۱۸۶۹          ج) ۱۷۰۱              د) ۱۹۲۹              هـ) ۱۳۹۹

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

↓↓↓↓

پاسخ معمای 'شش عنکبوت'

گزینه‌ی ج درست است.

در هر مرحله عدد نوشته شده در خانه‌ها پاک می‌شود ولی به عدد سه خانه‌ی دیگر اضافه می‌شود. پس در هر مرحله مجموع اعداد خانه‌ها سه برابر خواهد شد.

در ابتدا مجموع اعداد، ۲۱ است و پس از گذشت چهار ساعت برابر 21×81=1701 می‌شود.